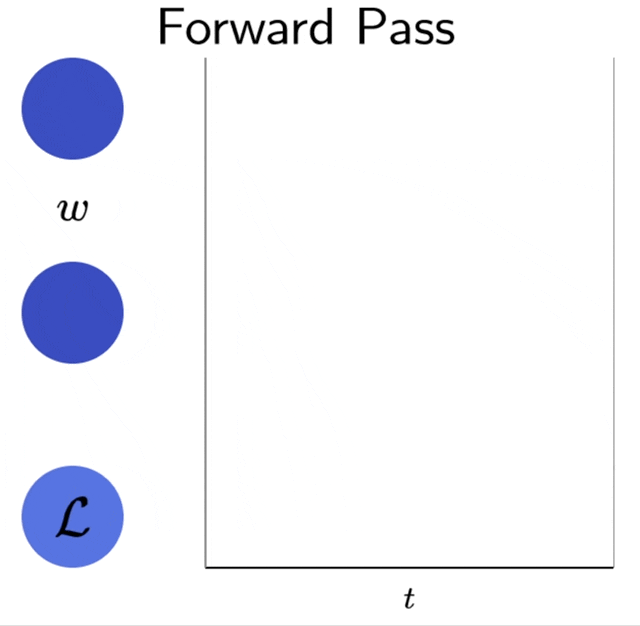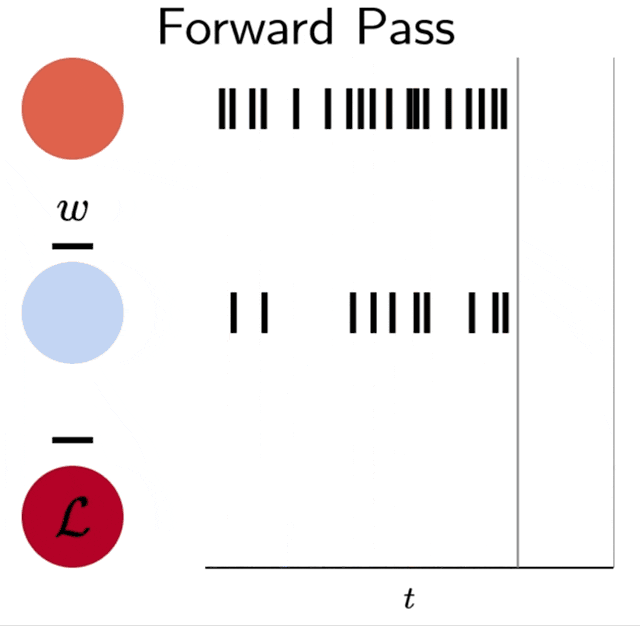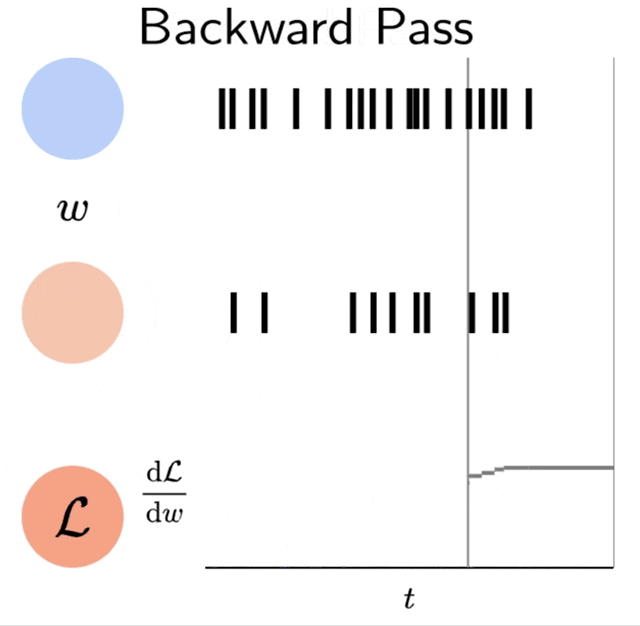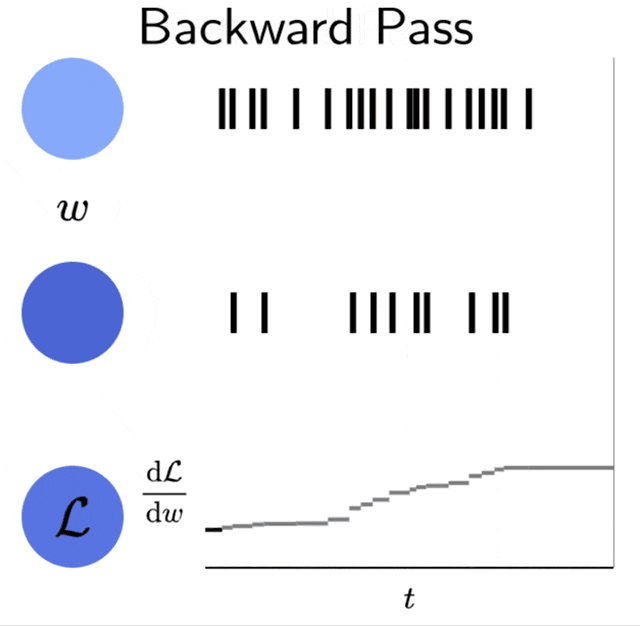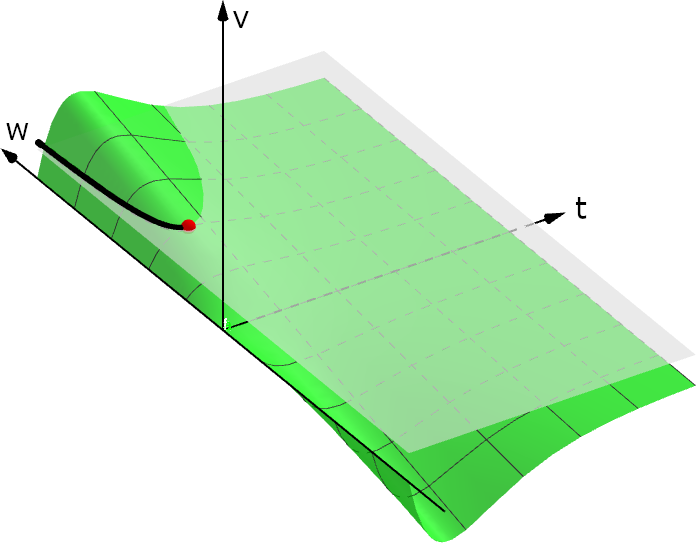
Event-based backpropagation in two spiking neurons and a spike-time dependent loss function \(\mathcal{L}\). The final accumulated value is \(\frac{\mathrm{d}\mathcal{L}}{\mathrm{d}w}\). This is a visualization of simulation data.

Spiking neurons communicate using discrete spike events which cause discontinuities in the neuron model’s dynamics. What are the implications for gradient-based optimization? Can we even have gradients?

In a spiking neural network composed of leaky integrate-and-fire neurons, gradients of membrane potentials and spike times exist and are finite almost everywhere in weight space, up to the hypersurfaces where spikes are added or lost. As recently shown by Christian Pehle and the author [1], deriving backpropagation to compute these gradients does not require any arbitrary choices or approximations. Furthermore, several recent publications demonstrate training of multi-layer spiking neural networks using exact gradients [1] [2] [3] [4] [5].

The event-based communication scheme of spiking neural networks can be retained during backpropagation (illustrated in the animation). This could allow novel neuromorphic hardware to achieve better scalability and energy efficiency compared to training non-spiking artificial neural networks on traditional digital hardware.

How is it possible that a discontinuous system can have well-defined parameter derivatives? What is the analogy to backpropagation for systems defined in continuous time such as spiking neural networks, as opposed to discrete time? This blog post answers these two questions, in that order.

Derivatives at Spikes

Spiking neural networks are hybrid dynamical systems: they combine continuous dynamics with event-triggered discontinuous state changes. Such systems typically model phenomena occuring on short timescales using instantaneous events. In the case of spiking neurons, this is the neuronal spike mechanism; other examples are a bouncing ball that is reflected upon hitting the ground, an engine transmission that changes its gear at a certain rotational speed or a thermostat that switches a heating element when a temperature threshold is reached.

Hybrid systems have been studied for the better half of a century within the context of optimal control theory [6], including the computation of parameter derivatives of state variables [7] [8]. The intuition is that if a small change to a parameter causes a small change of an event time, it causes a small change to state variables after the event. A formal mathematical treatment, as sketched in the following, makes this precise: it relates parameter derivatives before and after an event and states the conditions for when this relation holds.

The relation \(V(t, w)-\vartheta=0\) defines an implicit function (the black line) which allows us determine the spike time derivative \(\frac{\partial t_{\mathrm{spike}}}{\partial w}\).

In hybrid systems, events are triggered by zero-crossings of an event function. Consider a leaky integrate-and-fire neuron where the event function is simply \begin{align} V(t, w) - \vartheta, \end{align} where \(V(t, w)\) is the membrane potential at time \(t\) using synaptic weight \(w\) and \(\vartheta\) is the spike threshold. For simplicity, consider a single input spike at \(t=0\). The relation \(V(t, w) -\vartheta=0\) carves out a line in the \(t, w\) plane on which this relation holds (see figure on the left). This line is locally described by a function \(t_{\mathrm{spike}}(w)\). The implicit function theorem [9] allows us to express its derivative, the spike time derivative \(\frac{\partial t_{\mathrm{spike}}}{\partial w}\), in terms of the membrane potential derivatives: \begin{align} \boxed{\frac{\partial t_{\mathrm{spike}}}{\partial w} = - \frac{1}{\frac{\partial V}{\partial t}} \frac{\partial V}{\partial w}.} \end{align} Intuitively, changes of \(w\) need to be compensated by a change of \(t\) in order to stay on the line where \(V(t, w)-\vartheta=0\) holds. The rate of this change (left side of \((2)\)) is given by the negative ratio of the rates of change of \(V\) along the \(t\) and \(w\) axis (\(\frac{\partial V}{\partial t}\) and \(\frac{\partial V}{\partial w}\) in the right side of \((2)\)).

At a spike, we reset the membrane potential to zero. Denoting the membrane potential after the transition using \(V^+\), we have \begin{align} V^+(t_{\mathrm{spike}}, w) = 0. \end{align} We know that \(t_{\mathrm{spike}}\) is a function of the weight \(w\) and that its derivative satisfies \((2)\). Since our demand is that \((3)\) holds as we change \(w\) (implicitly changing \(t_{\mathrm{spike}}\)), the total derivative of \(V^+\) with respect to \(w\) must vanish: \begin{align} \frac{\partial V^+}{\partial w} + \frac{\partial t_{\mathrm{spike}}}{\partial w} \frac{\partial V^+}{\partial t} = 0. \end{align} Plugging in \((2)\) with \(V^-\) denoting evaluation before the spike and solving for \(\frac{\partial V^+}{\partial w}\) yields the desired result: \begin{align} \frac{\partial V^+}{\partial w} = \frac{\frac{\partial V^+}{\partial t}}{\frac{\partial V^-}{\partial t}} \frac{\partial V^-}{\partial w}. \end{align} In a leaky integrate-and-fire neuron with current-based synapses and membrane time constant \(\tau_{\mathrm{mem}}\), this can be written as [1] \begin{align} \boxed{\frac{\partial V^+}{\partial w} = \left(1+\frac{\vartheta}{\tau_{\mathrm{mem}}\frac{\partial V^-}{\partial t}}\right)\frac{\partial V^-}{\partial w}.} \end{align}

Inbetween spikes, the dynamics of \(\frac{\partial V}{\partial w}\) are given by differentiation with respect to \(w\) of the differential equations defining the dynamics of \(V\). At spikes, the derivatives jump according to \((6)\). These results generalize to a recurrent network of spiking neurons with arbitrarily many spikes [1].

The implicit function theorem requires that \(\dot{V}^- \neq 0\) in order for \((2)\) to hold. As the membrane potential becomes tangent to the threshold and we have \(\dot{V}^-\to 0\), the spike time derivative in \((2)\) diverges. Since the points where \(\dot V^- = 0\) and \(V^-=\vartheta\) holds are given by \((N-1)\)-dimensional hypersurfaces in the \(N\)-dimensional weight space (e.g., the red point in fig. 1), loss functions based on \(V\) or \(t_{\mathrm{spike}}\) are differentiable almost everywhere (similar to non-spiking neural networks with ReLUs that are non-differentiable at the “kink” of the activation). Published simulation results demonstrate that gradients can be used to optimize spiking neural networks [1] [2] [3] [4] [5].

Now that we have an idea of how to deal with spike discontinuities when computing parameter derivatives, what is the analogy to backpropagation that allows us to efficiently compute these derivatives?

The Adjoint Method

Backpropagation as used in deep learning is essentially a special case of the adjoint method [10] which can also be applied to continuous-time systems such as spiking neural networks or the recently introduced neural ordinary differential equations [11]. Given a set of dynamic variables defined by ordinary differential equations and a loss function, it specifies a set of adjoint variables that are computed in reverse time (“backpropagation through time”) and track the contribution of each variable to the total loss. The number of adjoint variables is equal to the number of original variables and, importantly, independent of the number of parameters, allowing for efficient gradient computation in systems with more parameters than state variables (e.g., neural networks).

History: Backprop Before Backprop Was a Thing

While the concept of adjoint differential equations can be traced back to Lagrange who showed their existence and uniqueness in the linear case in 1766 (équation adjointe, [12]), their use in optimal control theory and machine learning is more recent. The adjoint method was famously used by Lev Pontryagin in 1956 for his maximum principle that provides neccessary conditions for the optimality of control trajectories [13]. The first publications using the adjoint method to compute parameter gradients seem to be those written by Henry J. Kelley in 1960 [14] and Arthur E. Bryson in 1961 [15]. Both publications provide equations to backpropagate errors that are equivalent to those given in later derivations of backpropagation [16] [17] [18], which causes some to consider the latter to be independent discoveries of the “Kelley-Bryson gradient procedure” [19] [20].

Adjoint Variables = Backpropagated Errors

In non-spiking artificial neural networks, the adjoint variables simply correspond to what are typically called the intermediate variables or errors (\(\delta\)s) during backpropagation. Consider a feed-forward network with \(L\) layers and input \(x_0\). With activation \(x_i\), weight \(w_i\) at layer \(i\), activation function \(f\) and loss function \(\mathcal{L}(x_L)\) we have for \(i<L\):

\[\begin{array}{lr} \textrm{Forward} & \textrm{Backward/Adjoint} \\ x_{i+1} = f(w_{i+1}x_i)\quad\quad&\quad\quad\delta_{i} = w_{i+1}\delta_{i+1} f'(w_{i}x_{i-1}) \\ \mathcal{L}(x_L)&\delta_{L} = \frac{\partial \mathcal{L}(x_L)}{\partial x_L}f'(w_Lx_{L-1}) \end{array}\]

The derivative of \(\mathcal{L}(x_L)\) with respect to the weight \(w_i\) with \(1\leq i\leq L\) is then given as \begin{align} \frac{\mathrm{d}\mathcal{L}(x_L)}{\mathrm{d}w_i} = \delta_i x_{i-1}. \end{align}

Backprop in a Spiking Neural Network

Instead of discrete equations like these, spiking neural networks are defined by differential equations in continuous time and use spike events to couple neurons.

Consider a network of \(N\) leaky integrate-and-fire neurons coupled with weight matrix \(W\). With membrane potential \(V\), synaptic input \(I\) (both vectors of size \(N\)) and a loss function \begin{align} \mathcal{L}=l_p(t_{\mathrm{spike}})+\int_0^T l_V(V(t), t)\mathrm{d}t \end{align} that depends on the vector of spike times and membrane potentials, the free dynamics inbetween spikes are [1], denoting the adjoint variables using \(\lambda\),

\[\begin{array}{lr} \textrm{Forward} & \textrm{Backward/Adjoint} \\ \tau_{\mathrm{mem}}\dot{V} = -V + I\quad\quad&\quad\quad \tau_{\mathrm{mem}}\lambda_{V}' = -\lambda_{V} - \frac{\partial l_V}{\partial V}\\ \tau_{\mathrm{syn}}\dot{I} = - I\quad\quad&\tau_{\mathrm{syn}}\lambda_{I}' = -\lambda_{I} + \lambda_{V} \end{array}\]

where a dot denotes the time derivative \(\frac{\mathrm{d}}{\mathrm{d}t}\) and a dash denotes the reverse time derivative \(-\frac{\mathrm{d}}{\mathrm{d}t}\). Spikes cause the synaptic input \(I\) to jump as \begin{align} I^+ = I^- + We_n \end{align} where \(n\) is the index of the spiking neuron and \(e_n\) is the unit vector with a \(1\) at index \(n\). Using the partial derivative jumps such as those presented in the previous section, the jump of the \(n\)th component of \(\lambda_V\) turns out to be [1], with spike time \(t_{\mathrm{spike}}^k\),

\begin{align} (\lambda_V^-)_n = (\lambda_V^+)_n +\frac{1}{\tau_{\mathrm{mem}}(\dot{V}^-)_n}\left[\underbrace{\vartheta\lambda_V^+}_{\textrm{reset}}+\underbrace{\left(W^{\mathsf{T}}(\lambda_V^+-\lambda_I)\right)_n}_{\textrm{backpropagated errors}}+\underbrace{\frac{\partial l_p}{\partial t_{\mathrm{spike}}^k}}_{\textrm{spike time loss}}+\underbrace{l_V^--l_V^+}_{\textrm{voltage loss jump}}\right]. \end{align}

This equation couples adjoint variables at spike times using the term representing backpropagated errors. The only quantities that need to be stored during the forward pass are the \(n\)th component of \(\dot{V}^-\) and the spike time \(t_{\mathrm{spike}}^k\).

The derivative of \(\mathcal{L}\) with respect to weight \(w_{ji}\) that connects neuron \(i\) to neuron \(j\) is then given as a sum of the \(j\)th component of \(\lambda_I\) evaluated at the spike times of neuron \(i\), \begin{align} \frac{\mathrm{d}\mathcal{L}}{\mathrm{d}w_{ji}} = \sum_{\textrm{spikes from } i} (\lambda_I)_j. \end{align}

Since the adjoint variables are coupled only at spike times and gradients are computed by accumulating \(\lambda_I\) at spike times, the backward pass can be computed in an event-based fashion.

Conclusion

Gradients of spiking neural networks are well-defined and finite almost everywhere in weight space, up to the hypersurfaces where spikes are added or lost. These gradients can be efficiently computed using event-based backpropagation and used for gradient-based optimization. The event-based nature of backpropagation in spiking neural networks could allow neuromorphic hardware to retain the efficiency of spike-based processing during training.

References

Event-based backpropagation can compute exact gradients for spiking neural networks.
By Wunderlich, Timo C. and Pehle, Christian.
Published in Scientific Reports 2021 11:1, 11:1-17, Nature Publishing Group, 2021.
Fast and energy-efficient neuromorphic deep learning with first-spike times.
By Göltz, J. and Kriener, L. and Baumbach, A. and Billaudelle, S. and Breitwieser, O. and Cramer, B. and Dold, D. and Kungl, A. F. and Senn, W. and Schemmel, J. and Meier, K. and Petrovici, M. A..
Published in Nature Machine Intelligence 2021 3:9, 3:823-835, Nature Publishing Group, 2021.
Temporal Coding in Spiking Neural Networks with Alpha Synaptic Function.
By Comsa, Iulia M. and Fischbacher, Thomas and Potempa, Krzysztof and Gesmundo, Andrea and Versari, Luca and Alakuijala, Jyrki.
Published in ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing - Proceedings, 2020-May:8529-8533, Institute of Electrical and Electronics Engineers Inc., 2020.
Supervised learning based on temporal coding in spiking neural networks.
By Mostafa, Hesham.
Published in IEEE Transactions on Neural Networks and Learning Systems, 29:3227-3235, Institute of Electrical and Electronics Engineers Inc., 2018.
Temporal Backpropagation for Spiking Neural Networks with One Spike per Neuron.
By Kheradpisheh, Saeed Reza and Masquelier, Timothée.
Published in International Journal of Neural Systems, 30, World Scientific Publishing Company, 2020.
Modeling, simulation, sensitivity analysis, and optimization of hybrid systems.
By Barton, Paul I. and Lee, Cha Kun.
Published in ACM Transactions on Modeling and Computer Simulation (TOMACS), 12:256-289, ACM PUB27 New York, NY, USA , 2002.
Parametric sensitivity functions for hybrid discrete/continuous systems.
By Galán, Santos and Feehery, William F. and Barton, Paul I..
Published in Applied Numerical Mathematics, 31:17-47, North-Holland, 1999.
General sensitivity equations of discontinuous systems.
By Rozenvasser, E. N..
Published in Autom. Remote Control, 1967:400–404, Springer US, New York, NY; Pleiades Publishing, New York, NY; MAIK “Nauka/Interperiodica”, Moscow, 1967.
The Implicit Function Theorem: History, Theory, and Applications.
By Krantz, Steven G. and Parks, Harold R..
Springer New York, 2013.
ISBN: 9781461459811.
A theoretical framework for back-propagation.
By Lecun, Yann.
In Proceedings of the 1988 Connectionist Models Summer School, CMU, Pittsburg, PA, pages 21–28, Morgan Kaufmann, 1988.
Neural Ordinary Differential Equations.
By Chen, Ricky T. Q. and Rubanova, Yulia and Bettencourt, Jesse and Duvenaud, David K.
In Advances in Neural Information Processing Systems, 31, pages , Curran Associates, Inc., 2018.
Solution de différents problèmes de calcul intégral.
By Lagrange, Joseph-Louis.
In Miscellanea taurinensia, Société royale de Turin, 1766.
The maximum principle in the theory of optimal processes of control.
By Boltyanski, V.G. and Gamkrelidze, R.V. and Mishchenko, E.F. and Pontryagin, L.S..
Published in IFAC Proceedings Volumes, 1(1):464-469, 1960.
Gradient Theory of Optimal Flight Paths.
By Kelley, Henry J..
Published in ARS Journal, 30(10):947-954, 1960.
A gradient method for optimizing multi-stage allocation processes.
By Bryson, A.E..
In Proceedings of a Harvard Symposium on Digital Computers and Their Applications, 1961.
Taylor expansion of the accumulated rounding error.
By Linnainmaa, Seppo.
Published in BIT Numerical Mathematics, 16:146-160, 1976.
Applications of advances in nonlinear sensitivity analysis.
By Werbos, Paul J..
In System Modeling and Optimization, pages 762–770, Springer Berlin Heidelberg, 1982.
Learning Internal Representations by Error Propagation.
By Rumelhart, David E. and McClelland, James L..
In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations, pages 318-362, 1987.
Artificial neural networks, back propagation, and the Kelley-Bryson gradient procedure.
By Dreyfus, Stuart E..
Published in Journal of Guidance, Control, and Dynamics, 13(5):926-928, 1990.
On derivation of MLP backpropagation from the Kelley-Bryson optimal-control gradient formula and its application.
By Mizutani, E. and Dreyfus, S.E. and Nishio, K..
In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, 2, pages 167-172 vol.2, 2000.